Definitions
The two simplest sequences to work with are arithmetic and geometric sequences. An arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value. For instance, 2, 5, 8, 11, 14,... and 7, 3, –1, –5,... are arithmetic, since you add 3 and subtract 4, respectively, at each step. A geometric sequence goes from one term to the next by always multiplying (or dividing) by the same value. So 1, 2, 4, 8, 16,... and 81, 27, 9, 3, 1, 1/3,... are geometric, since you multiply by 2 and divide by 3, respectively, at each step.
The number added (or subtracted) at each stage of an arithmetic sequence is called the "common difference" d, because if you subtract (find the difference of) successive terms, you'll always get this common value. The number multiplied (or divided) at each stage of a geometric sequence is called the "common ratio" r, because if you divide (find the ratio of) successive terms, you'll always get this common value.
 Unit 8 Table of Contents
Unit 8 Table of Contents Arithmetic Sequences and Series Overview
Arithmetic Sequences and Series Overview Formulas for Arithmetic Sequences and Series
Formulas for Arithmetic Sequences and Series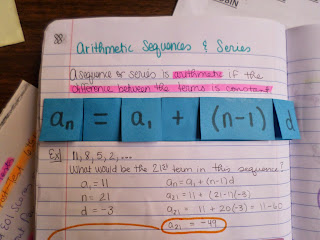 nth Term Foldable (Arithmetic) - Outside)
nth Term Foldable (Arithmetic) - Outside)
nth Term Foldable (Arithmetic) - Inside

Sum of the first n terms (Arithmetic) Foldable - Outside

Sum of the first n terms (Arithmetic) Foldable - Inside

Additional Practice with Arithmetic Sequences & Series
 Geometric Sequences and Series Formulas
Geometric Sequences and Series Formulas Additional Practice with Geometric Sequences and Series
Additional Practice with Geometric Sequences and Series
nth Term Foldable (Geometric) - Outside

nth Term Foldable (Geometric) - Inside
 Sum of the first n terms (Geometric) Foldable - Outside
Sum of the first n terms (Geometric) Foldable - Outside
Sum of the first n terms (Geometric) Foldable - Inside
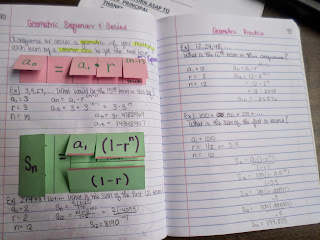
Geometric Sequences and Series Overview

 Series Frayer Model
Series Frayer Model
No comments:
Post a Comment